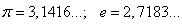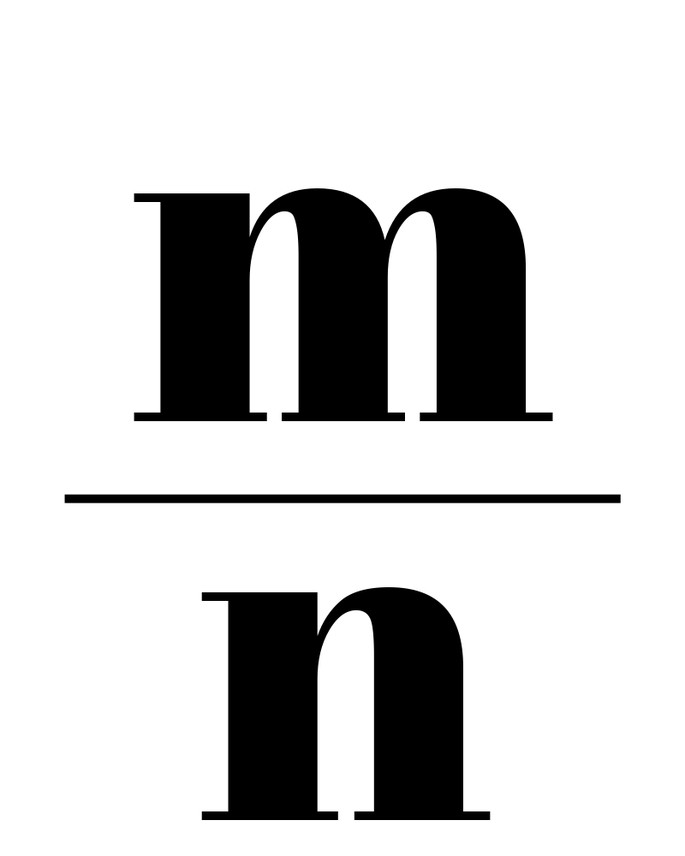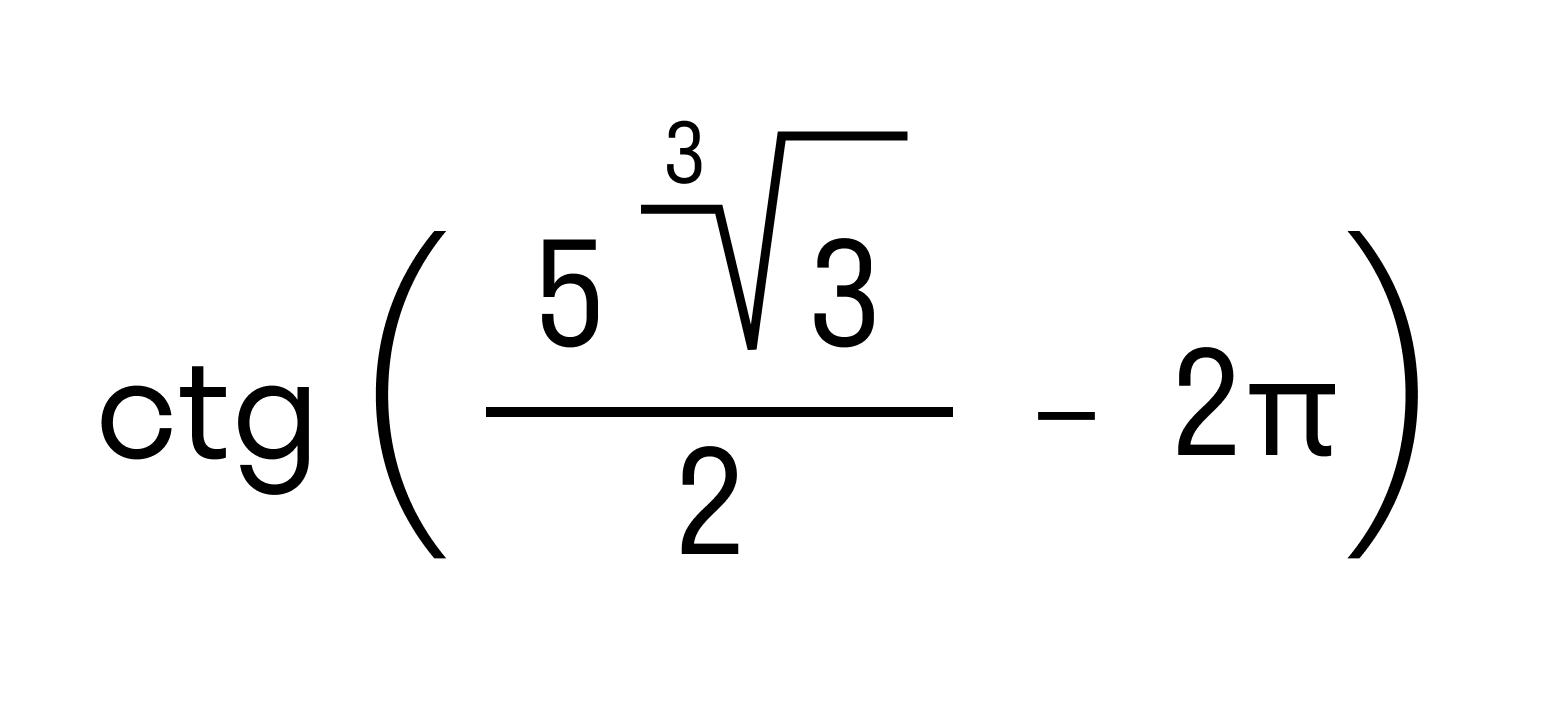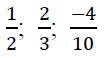недействительные числа это какие
Математика
Тестирование онлайн
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Округлить 8,759123. с точностью до целой части.
Округлить 8,759123. с точностью до десятой части.
Округлить 8,759123. с точностью до сотой части.
Округлить 8,759123. с точностью до тысячной части.
Иррациональные числа
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
Действительные числа
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
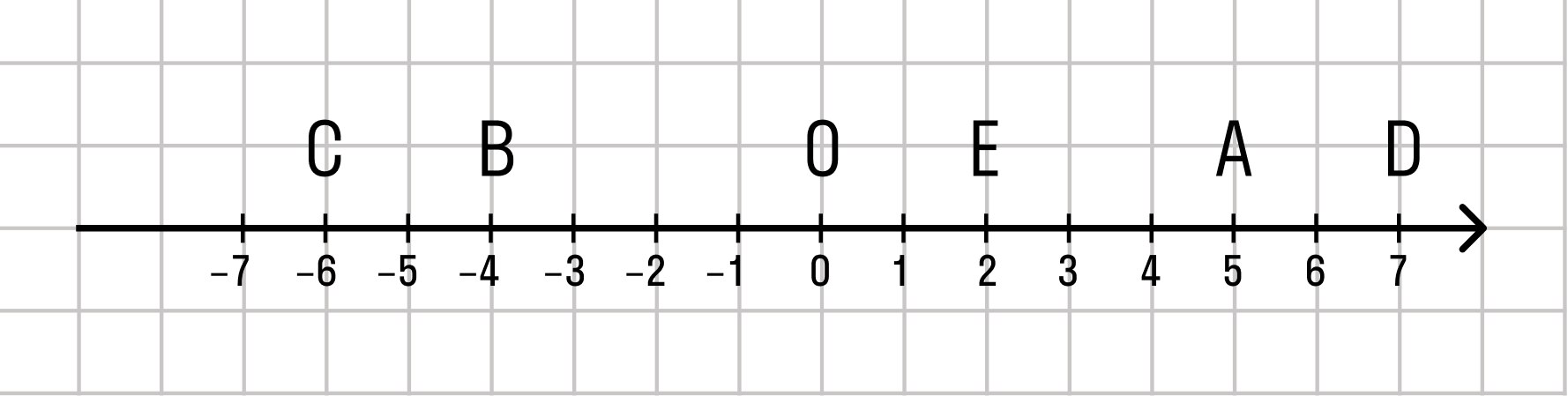
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Виды чисел.
У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.
Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…
Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…
Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: 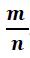
где m−целое число (числитель), n – натуральное число (знаменатель).
Например:
Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида 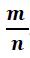
Например: √2; √5; π; e
Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:
Видно их вложенность друг в друга.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Действительные числа: определение, примеры, представления
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Данное определение можно записать иначе с учетом следующего:
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.