Коллизия что это в программировании
Коллизия хэш-функции
Коллизией хеш-функции H называется два различных входных блока данных x и y таких, что H(x) = H(y).
Содержание
Коллизии криптографических хеш-функций
Мерой криптостойкости хеш-функции является вычислительная сложность нахождения коллизии. Так как криптографические хеш-функции используются для подтверждения неизменности исходной информации (например, для создания цифровой подписи), то найти коллизию для них должно быть сложно (не проще чем полным перебором).
Для криптографических хеш-функций различают два типа стойкости к нахождению коллизий:
Также ключевым свойством хеш-функций является их необратимость:
На этом свойстве основано большинство методов применения хеш-функций в криптографии. В качестве примера можно рассмотреть простую процедуру аутентификации пользователя: при регистрации в системе пользователь вводит свой пароль, к которому применяется хеш-функция и результат записывается в базу данных; далее при каждом вводе пароля, он хешируется и результат сравнивается с тем, который записан в БД. При таком подходе даже если злоумышленник получит доступ к базе данных, он не сможет восстановить исходные пароли пользователей (при условии того, что обеспечено свойство необратимости хеш-функции). Однако, если злоумышленник умеет находить коллизии для этой хеш-функции, ему не составит труда найти поддельный пароль, который будет иметь хеш одинаковый с паролем пользователя.
Разрешение коллизий в хеш-таблицах
Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют специальные методики для преодоления возникающих сложностей:
Разрешение коллизий
Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.
Содержание
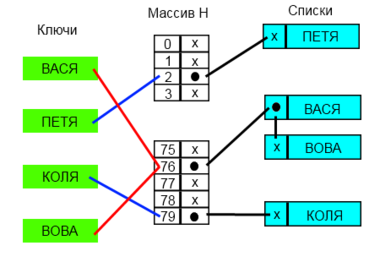
Разрешение коллизий с помощью цепочек [ править ]
Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.
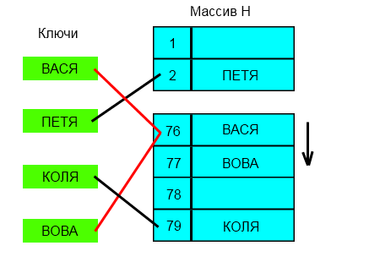
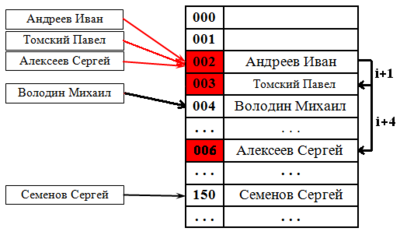
Линейное разрешение коллизий [ править ]
Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.
Стратегии поиска [ править ]
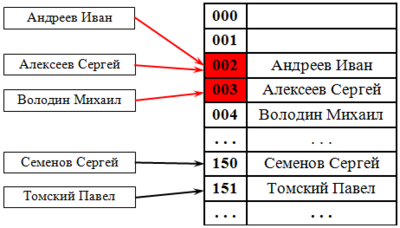
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.
Проверка наличия элемента в таблице [ править ]
Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.
При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.
Проблемы данных стратегий [ править ]
Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.
Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.
Удаление элемента без пометок [ править ]
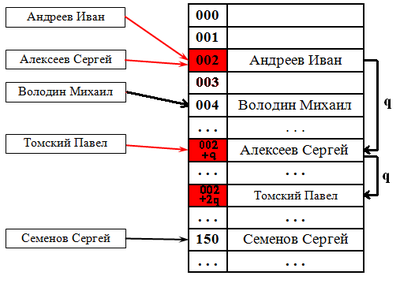
Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:
Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).
Хеш-таблицу считаем зацикленной
| Утверждение (о времени работы): |
| [math]\triangleright[/math] |
| Заметим что указатель [math]j[/math] в каждой итерации перемещается вперёд на [math]q[/math] (с учётом рекурсивных вызовов [math]\mathrm |
| [math]\triangleleft[/math] |
Вариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций
Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.
Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm
Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.
Двойное хеширование [ править ]
Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.
Принцип двойного хеширования [ править ]
[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]
Выбор хеш-функций [ править ]
[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:
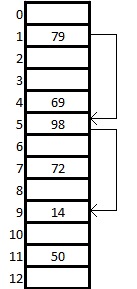
Пример [ править ]
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:
[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]
[math] h_1(k) = k \bmod 13 [/math]
[math] h_2(k) = 1 + k \bmod 11 [/math]
Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.
Простая реализация [ править ]
Реализация с удалением [ править ]
Альтернативная реализация метода цепочек [ править ]
Что нужно знать об устройстве коллекций, основанных на хешировании
Всем привет. На связи Владислав Родин. В настоящее время я являюсь руководителем курса «Архитектор высоких нагрузок» в OTUS, а также преподаю на курсах, посвященных архитектуре ПО.
Помимо преподавания, как вы могли заметить, я занимаюсь написанием авторского материала для блога OTUS на хабре и сегодняшнюю статью хочу посвятить запуску нового потока курса «Алгоритмы для разработчиков».
Введение
Постановка задачи
Давайте зададимся целью создать структуру данных, которая позволяет:
Массив
Попробуем сделать эти операции поверх массива, который является самой простой структурой данных. Договоримся, что будем считать ячейку пустой, если в ней содержится null.
Проверка наличия
Необходимо сделать линейный поиск по массиву, ведь элемент потенциально может находиться в любой ячейке. Асимптотически это можно осуществить за O(n), где n — размер массива.
Добавление
Если нам надо добавить элемент абы куда, то вначале мы должны найти пустую ячейку, а затем записать в нее элемент. Таким образом, мы опять осуществим линейный поиск и получим асимптотику O(n).
Удаление
Чтобы удалить элемент, его нужно сначала найти, а затем в найденную ячейку записать null. Опять линейный поиск приводит нас к O(n).
Простейшее хеш-множество
Обратите внимание, что при каждой операции, мы сначала искали индекс нужной ячейки, а затем осуществляли операцию, и именно поиск портит нам асимптотику! Если бы мы научились получать данный индекс за O(1), то исходная задача была бы решена.
Давайте теперь заменим линейный поиск на следующий алгоритм: будем вычислять значение некоторой фунции — хеш-функции, ставящей в соответствие объекту класса некоторое целое число. После этого будем сопоставлять полученное целое число индексу ячейки массива (это достаточно легко сделать, например, взяв остаток от деления этого числа на размер массива). Если хеш-функция написана так, что она считается за O(1) (а она так обычно и написана), то мы получили самую простейшую реализацию хеш-множества. Ячейка массива в терминах хеш-множества может называться bucket‘ом.
Проблемы простейшей реализации хеш-множества
Как бы ни была написана хеш-функция, число ячеек массива всегда ограничено, тогда как множество элементов, которые мы хотим хранить в структуре данных, неограничено. Ведь мы бы не стали заморачиваться со структурой данных, если бы была потребность в сохранении всего лишь десяти заранее известных элементов, верно? Такое положение дел приводит к неизбежным коллизиям. Под коллизией понимается ситуация, когда при добавлении разных объектов мы попадаем в одну и ту же ячейку массива.
Для разрешения коллизий придумано 2 метода: метод цепочек и метод открытой адресации.
Метод цепочек
Метод цепочек является наиболее простым методом разрешения коллизий. В ячейке массива мы будем хранить не элементы, а связанный список данных элементов. Потому как добавление в начало списка (а нам все равно в какую часть списка добавлять элемент) обладает асимптотикой О(1), мы не испортим общую асимптотику, и она останется равной О(1).
У данной реализации есть проблема: если списки будут очень сильно вырастать (в качестве крайнего случая можно рассмотреть хеш-функцию, которая возвращает константу для любого объекта), то мы получим асимптотику O(m), где m — число элементов во множестве, если размер массива фиксирован. Для избежания таких неприятностей вводится понятие коэффициент заполнения (он может быть равен, например, 1.5). Если при добавлении элемента оказывается, что доля числа элементов, находящихся в структуре данных по отношению к размеру массива, превосходит коэффициент заполнения, то происходит следующее: выделяется новый массив, размер которого превосходит размер старого массива (например в 2 раза), и структура данных перестраивается на новом массиве.
Данный метод разрешения коллизий и применяется в Java, а структура данных называется HashSet.
Метод открытой адресации
В данном методе в ячейках хранятся сами элементы, а в случае коллизии происходит последовательность проб, то есть мы начинаем по некоторому алгоритму перебирать ячейки в надежде найти свободную. Это можно делать разными алгоритмами (линейная / квадратичная последовательности проб, двойное хеширование), каждый из которых обладает своими проблемами (например, возникновение первичных или вторичных кластеров).
От хеш-множества к хеш-таблице (HashMap)
Давайте создадим структуру данных, которая позволяет так же быстро, как и хеш-множество (то есть за O(1)), добавлять, удалять, искать элементы, но уже по некоторому ключу.
Воспользуемся той же структурой данных, что у хеш-множества, но хранить будем не элементы, а пары элементов.
Таким образом, вставка (put(Key key, Value value)) будет осуществляться так: мы посчитаем ячейку массива по объекту типа Key, получим номер bucket’а. Пройдемся по списку в bucket’е, сравнивая ключ с ключом в хранимых парах. Если нашли такой же ключ — просто вытесняем старое значение, если не нашли — добавляем пару.
Как осуществляется получение элемента по ключу? Да по похожему принципу: получаем bucket по ключу, проходимся по парам и возвращаем значение в паре, ключ в которой равен ключу в запросе, если такая пара есть, и null в противном случае.
Данная структура данных и называется хеш-таблицей.
Типичные вопросы на собеседовании
Q: Как устроены HashSet и HashMap? Как осуществляются основные операциии в данных коллекциях? Как применяются методы equals() и hashCode()?
A: Ответы на данные вопросы можно найти выше.
Q: Каков контракт на equals() и hashCode()? Чем он обусловлен?
A: Если объекты равны, то у них должны быть равны hashCode. Таким образом, hashCode должен определяться по подможноству полей, учавствующих в equals. Нарушение данного контракта может приводить к весьма интересным эффектам. Если объекты равны, но hashCode у них разный, то вы можете не достать значение, соответствующее ключу, по которому вы только что добавили объект в HashSet или в HashMap.
Вывод
На собеседованиях очень любят задавать различные кейсы, связанные с этими структурами данных. При этом решение любого из них может быть выведено из понимания принципов их работы без всякой «зубрежки».
На этом все. Если вы дочитали материал до конца, приглашаю на бесплатный урок по теме «Секреты динамического программирования» в рамках урока мой коллега — Евгений Волосатов покажет как решить олимпиадную задачу используя идеи динамического программирования.
Box2d: анатомия коллизий
Что такое коллизии?
В Box2D принято считать, что друг с другом сталкиваются тела, однако на самом деле при расчете коллизий используются фикстуры (fixtures, переводы слова существуют, но я не уверен, есть ли среди них устоявшийся). Объекты могут сталкиваться разными способами, поэтому библиотека предоставляет большое количество уточняющей информации, которая может быть использована в игровой логике. Например, вы можете захотеть узнать следующее:
Все настроено таким образом, чтобы нижняя часть треугольника столкнулась с верхним углом квадрата. Тонкости реализации этого процесса выходят за рамки статьи — основное внимание уделим тому, какую информацию можно извлечь на каждом этапе столкновения. Если есть желание самостоятельно запустить предлагаемый пример, исходный код прилагается.
Получении информации о столкновении
Информация о столкновении содержится в объекте типа b2Contact. Из него можно узнать, какие именно фикстуры сталкиваются, и определить их положение и направление результирующих импульсов. Существует два способа получения объектов b2Contact в Box2D. Первый — перебрать текущий список контактов каждого тела объекта, второй — использовать слушатель контактов. Рассмотрим каждый из них, чтобы дальше было понятнее, о чем идет речь.
Проверка списка контактов
В любой момент можно перебрать все контакты мира (имеется в виду b2World)
или получить контакты тела определенного объекта
Если выбран этот подход, очень важно помнить, что наличие контакта в этих списках не означает, что фикстуры соприкасаются — это значит только, что пересекаются их AABB. Если требуется убедиться, что контактируют сами фикстуры, воспользуйтесь методом IsTouching(). К этому вопросу мы еще вернемся.
Слушатели контактов
Проверка списка контактов становится неэффективной в ситуациях, когда столкновения происходят часто и в больших количествах. Устанавливая слушателей контактов, вы отдаете поручение Box2D сообщать, когда происходит что-то интересное, вместо того, чтобы вручную следить за началом и завершением столкновений. Слушатель контактов — это объект класса b2ContactListener, часть функций которого замещается при необходимости.
Должен заметить, что в зависимости от ситуации, некоторые события дают нам не только объект b2Contact. В процессе выполнения функции Step, когда Box2D определяет, что произошел контакт, он выполняет обратный вызов определенных функций слушателя, чтобы уведомить вас. Практическое использование «обратных вызовов при коллизиях» рассматривается в отдельной статье. Здесь мы все внимание сосредоточим на том, что можно узнать, обрабатывая события столкновений.
В общем случае я рекомендую метод слушателей контактов. На первый взгляд он может показаться несколько неуклюжим, однако он более эффективен и полезен в долгосрочной перспективе. До сих пор мне не встречалась ситуация, когда проверка списка контактов давала бы ощутимый выигрыш.
Вне зависимости от способа получения контактов, они содержат одинаковую информацию. Наиболее важные данные о пересекающихся фикстурах можно получить так
Когда происходит обход списка контактов определенного объекта, возможно, одна из фикстур коллизии известна, но если используется слушатель контактов, придется полностью положиться на эти функции, чтобы понять, что с чем сталкивается. Четко заданного порядка фикстур не существует, так что часто приходится устанавливать пользовательские данные (user data), чтобы понять, какому именно объекту принадлежит фикстура или тело. Располагая объектом фикстуры, можно воспользоваться методом GetBody(), чтобы получить ссылку на тело.
Столкновение шаг за шагом.
Теперь давайте подробнее рассмотрим последовательность событий, происходящих при столкновении. Надеюсь, картинок с описанием каждого шага будет достаточно для понимания материала. Возможно, вы захотите загрузить исходники к уроку, чтобы запускать их во время чтения. Тестовая программа позволяет ставить симуляцию на паузу, перезапускать и выполнять ее по шагам.
Начнем с ситуации, когда AABB фикстур не пересекаются, так мы сможет проследить историю полностью. Кликните флажок «AABBs», чтобы увидеть фиолетовые прямоугольные области вокруг каждой фикстуры.
AABB фикстур начинают перекрываться
Несмотря на то, что сами фикстуры еще не пересеклись, на этом этапе уже создается экземпляр b2Contact и добавляется в список контактов мира и списки каждого тела. Если вы просматриваете эти списки, то по наличию объектов b2Contact можно судить о том, что в принципе контакт возможен, хотя фикстуры не обязательно пересеклись.
Результат: контакт существует, но IsTouching() возвращает ложь
Продолжаем симуляцию, пока не пересекутся непосредственно фикстуры…
Фикстуры начинают пересекаться.
Приблизив верхний угол квадрата, можно увидеть переход, как на следующих изображениях
Шаг n
Шаг n+1 (не bullet-объекты)
Все это происходит за один шаг симуляции, значит, реальную точку пересечения (к которой ведет пунктирная линия на рисунке выше), мы проскочили. Это происходит потому, что Box2D сначала смещает все тела и только потом проверяет пересечения, по крайней мере, это его поведение по умолчанию. Если вам нужна реальная точка соприкосновения, то нужно сделать следующее
Шаг n+1 (треугольник — bullet-объект)
Bullet-тела, расходуют больше процессорного времени на расчеты и для большинства приложений не требуются. Просто помните о том, что при обычных настройках, иногда коллизии могут пропускаться — в нашем примере, если бы треугольник двигался достаточно быстро, он мог бы пролететь сквозь угол квадрата, не инициировав столкновения. Если у вас есть очень быстро перемещающиеся тела, контакты которых не должны пропускаться, например, мммм… пули 🙂 тогда их нужно объявлять как bullet-объекты. Дальнейшее изложение будет вестись для не-bullet-тел.
Точки столкновения и нормаль
К этому моменту в нашем контакте присутствует реальное соприкосновение, что дает возможность ответить не некоторые вопросы в начале статьи. Для начала давайте получим нормаль и точку касания. Предполагается, что приведенный далее код вызывается или из метода BeginContact слушателя контактов или из вашего метода после предварительного получения контакта из списка.
Объект контакта содержит информацию о коллизии в локальных координатах тел сталкивающихся объектов, а это не совсем то, что нам нужно. Однако можно запросить у контакта более полезную структуру b2WorldManifold, которая содержит позицию коллизии в мировых координатах.
Полученные точки будут использованы Box2D для расчета реакции на столкновение для вычисления импульса, который направит фикстуры в противоположные стороны. Это будут неточные места соприкосновения фикстур (если только вы не использовали bullet-объекты), хотя на практике их обычно достаточно для расчетов столкновений в игровой логике.
Далее рассмотрим нормаль коллизии, которая направлена от фикстуры A к B:
Похоже на то, что для этого столкновения самый быстрый способ избавиться от перекрывающихся объектов, это оттолкнуть угол треугольника вверх и влево, а квадрата — вниз и вправо. Хотелось бы обратить ваше внимание на то, что нормаль — это просто направление, она не привязана ни к какой точке контакта — я изобразил ее проходящей через points[0] для удобства.
Важно также помнить, что нормаль столкновения не определяет угол между фикстурами (ведь треугольник двигается вообще горизонтально) — она лишь задает направление, следуя которому быстрее всего компенсируется перекрытие объектов. Например, представьте, что треугольник двигается немного быстрее, и перекрытие выглядит так:
Тогда самый быстрый способ разделить фикстуры — оттолкнуть треугольник вверх и вправо. Так что использовать нормаль для расчета угла между объектами нецелесообразно. Если требуется узнать направления, по которым будут разделяться фигуры, можно воспользоваться следующим кодом:
Он позволит получить относительную скорость реакции всех точек столкнувшихся тел. В нашем простом случае можно было бы ограничиться линейной скоростью треугольника, так как известно, что квадрат неподвижен, а треугольник не вращается. Но вышеуказанный код будет учитывать и случаи, когда оба дела движутся или вращаются.
Также нужно заметить, что не при каждом столкновении будет именно две точки коллизии. Я намерено остановился на достаточно сложном примере, когда перекрываются два угла многоугольников, но чаще бывает только одна такая точка. Вот несколько примеров столкновений, для которых достаточно одной точки
Итак, только что мы рассмотрели, как определить точки и нормаль коллизии, на основе которых Box2D будет рассчитывать реакцию, направленную на компенсацию перекрытий. Теперь вернемся к последовательности событий.
Реакция на столкновение
( (b2Contact::Update, b2Island::Report))
Шаг_столкновения
Шаг_столкновения + 1
Шаг_столкновения + 1
Когда фикстуры перекрываются, реакция Box2d по умолчанию — приложить импульс к каждой из них, чтобы направить в разные стороны. Однако это не всегда удается сделать за один шаг моделирования. Как показано на рисунках для нашего примера, две фикстуры будут перекрываться на протяжении трех шагов, пока отскок не состоится, и они окончательно не разделятся.
В это время мы можем вмешаться и настроить поведение модели, как нам захочется. Если используется подход со слушателем контактов, методы PreSolve и PostSolve будут вызываться на каждом шаге, пока фикстуры перекрываются, давая возможность модифицировать контакт перед тем, как он будет обработан стандартными средствами реакции на коллизию (PreSolve), и узнать, какие импульсы были приложены Box2D (PostSolve)
Для большей наглядности приведу вывод printf, которая помещена в в функцию Step и каждый метод слушателя контактов:
Результат: PreSolve and PostSolve вызываются несколько раз
PreSolve and PostSolve
Оба эти метода получают в качестве параметра указатель на b2Contact, так что мы имеем доступ к той же информации о точках и нормалях, что и в BeginContact. PreSolve дает на возможность изменить характеристики контакта перед расчетом реакции на столкновение и даже отменить реакцию полностью. PostSolve позволяет получить информацию о вычисленной реакции.
В PreSolve можно сделать следующие настройки объекта контакта:
Вызов SetEnabled(false) деактивирует контакт, значит, реакция на столкновение просчитываться не будет. Это может понадобиться, когда необходимо временно позволить объектам пролетать друг сквозь друга. Классический пример — односторонняя стена или платформа, когда игрок может пройти сквозь обычно непроходимый объект при определенных условиях, которые можно проверить только во время выполнения — например, позиция игрока или направление его движения.
Важно помнить, что на следующей итерации контакт снова активируется, так что если нужно отключить его на продолжительное время, придется делать это на каждом шаге.
Кроме ссылки на контакт, PreSolve содержит второй параметр, из которого можно получить характеристики коллизии (точки и нормаль) с предыдущего шага моделирования. Если кто-то знает, зачем это может пригодиться — расскажите мне 😀
PostSolve вызывается после того, как реакция на столкновение была рассчитана и применена. У метода есть второй параметр, содержащий информацию о приложенном в результате импульсе. Обычно он используется для проверки, не превысила ли реакция некоторое пороговое значения, в результате чего объект можно разрушить и т.п. В статье » sticky projectiles» содержится пример использования функции PostSolve для определения, должна ли стрела застревать в мишени.
Возвращаемся к сценарию столкновения
Фикстуры больше не перекрываются
(b2Contact::Update)
AABB все еще перекрываются, так что контакт пока остается в соответствующих списках мира и тела.
(увеличенный масштаб)
AABB фикстур не перекрываются
(b2ContactManager::Collide)
Результат: контакт удаляется из списка контактов мира и тела.
Метод EndContact получает указатель на b2Contact, когда фикстуры уже не соприкасаются, так что в нем уже не содержится актуальной информации. Тем не менее EndContact является неотъемлемым элементом слушателя контактов, так как позволяет контролировать, когда игровые объекты покидают зону соприкосновения.